Mixture Methods

Gaussian Mixture Models (GMMs) are flexible building blocks for other machine learning algorithms. This is in part because they are great approximations for general probability distributions but also because they remain somewhat interpretable even when the dataset gets very complex. This package makes use of GMMs to construct other algorithms.

Classification

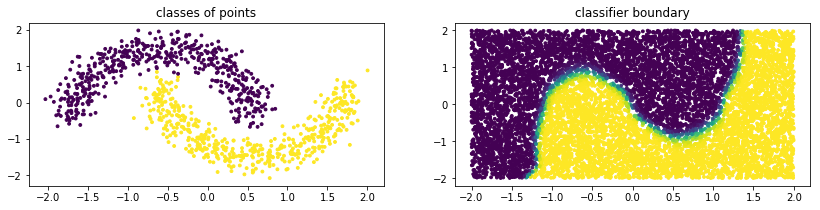
Below is some example code of how you might use a GMM from sklego to perform classification.

import numpy as np
import matplotlib.pylab as plt

from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler

from sklego.mixture import GMMClassifier

n = 1000
X, y = make_moons(n)
X = X + np.random.normal(n, 0.12, (n, 2))
X = StandardScaler().fit_transform(X)
U = np.random.uniform(-2, 2, (10000, 2))

mod = GMMClassifier(n_components=4).fit(X, y)

plt.figure(figsize=(14, 3))
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], c=mod.predict(X), s=8)
plt.title("classes of points");

plt.subplot(122)
plt.scatter(U[:, 0], U[:, 1], c=mod.predict_proba(U)[:, 1], s=8)
plt.title("classifier boundary");
_images/outlier-clf.png

Outlier Detection

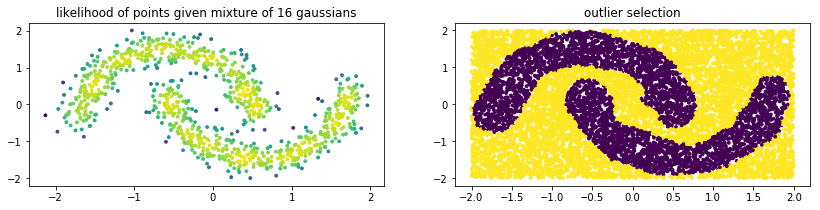
Below is some example code of how you might use a GMM from sklego to do outlier detection. Note that the GMM outlier detection generates prediction values that are either -1 (outlier) or +1 (normal).

import numpy as np
import matplotlib.pylab as plt

from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler

from sklego.mixture import GMMOutlierDetector

n = 1000
X = make_moons(n)[0] + np.random.normal(n, 0.12, (n, 2))
X = StandardScaler().fit_transform(X)
U = np.random.uniform(-2, 2, (10000, 2))

mod = GMMOutlierDetector(n_components=16, threshold=0.95).fit(X)

plt.figure(figsize=(14, 3))
plt.subplot(121)
plt.scatter(X[:, 0], X[:, 1], c=mod.score_samples(X), s=8)
plt.title("likelihood of points given mixture of 16 gaussians");

plt.subplot(122)
plt.scatter(U[:, 0], U[:, 1], c=mod.predict(U), s=8)
plt.title("outlier selection")
_images/outlier-mixture.png

Note that with a GMM there are multiple ways to select outliers. Instead of selection points that are beyond the likely quantile threshold one can also specify the number of standard deviations away from the most likely standard deviations a given point it.

plt.figure(figsize=(14, 3))
for i in range(1, 5):
    mod = GMMOutlierDetector(n_components=16, threshold=i, method="stddev").fit(X)
    plt.subplot(140 + i)
    plt.scatter(U[:, 0], U[:, 1], c=mod.predict(U), s=8)
    plt.title(f"outlier sigma={i}");
_images/outlier-mixture-stddev.png

Detection Details

The outlier detection methods that we use are based on the likelihoods that come out of the estimated Gaussian Mixture. Depending on the setting you choose we have a different method for determining if a point is inside or outside the threshold.

  1. If the “quantile” method is used we take all the likelihood scores found that the GMM associates on a training dataset to determine where to set a threshold. The threshold value must be between 0 and 1 here.

  2. If the “stddev” method is used then the threshold value is now interpreted as the number of standard deviations lower than the mean we are. We only calculate the standard deviation on the lower scores because there’s usually more variance here. Note that this setting allows you to be much more picky in selecting than the “quantile” setting since this method allows you to be more exclusive than the “quantile” method with threshold equal to one.

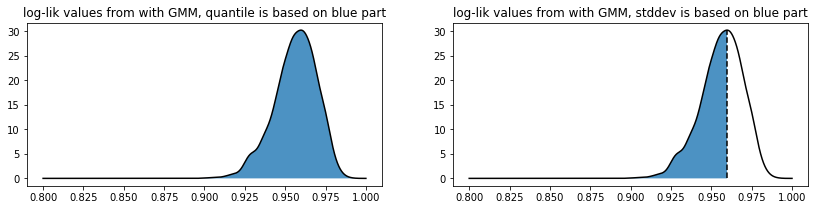
_images/outlier-mixture-threshold.png

As a sidenote: this image was generated with some dummy data, but its code can be found below.

import numpy as np
import matplotlib.pylab as plt
from scipy.stats import gaussian_kde

score_samples = np.random.beta(220, 10, 3000)
density = gaussian_kde(score_samples)
likelihood_range = np.linspace(0.80, 1.0, 10000)

index_max_y = np.argmax(density(likelihood_range))
mean_likelihood = likelihood_range[index_max_y]
new_likelihoods = score_samples[score_samples < mean_likelihood]
new_likelihoods_std = np.sqrt(np.sum((new_likelihoods - mean_likelihood) ** 2)/(len(new_likelihoods) - 1))

plt.figure(figsize=(14, 3))
plt.subplot(121)
plt.plot(likelihood_range, density(likelihood_range), 'k')
xs = np.linspace(0.8, 1.0, 2000)
plt.fill_between(xs, density(xs), alpha=0.8)
plt.title("log-lik values from with GMM, quantile is based on blue part");

plt.subplot(122)
plt.plot(likelihood_range, density(likelihood_range), 'k')
plt.plot([mean_likelihood, mean_likelihood], [0, density(mean_likelihood)], 'k--')
xs = np.linspace(0.8, mean_likelihood, 2000)
plt.fill_between(xs, density(xs), alpha=0.8)
plt.title("log-lik values from with GMM, stddev is based on blue part");